Блог вчителя математики Лисенко Тетяни Андріївни: марта 2021

среда, 31 марта 2021 г.

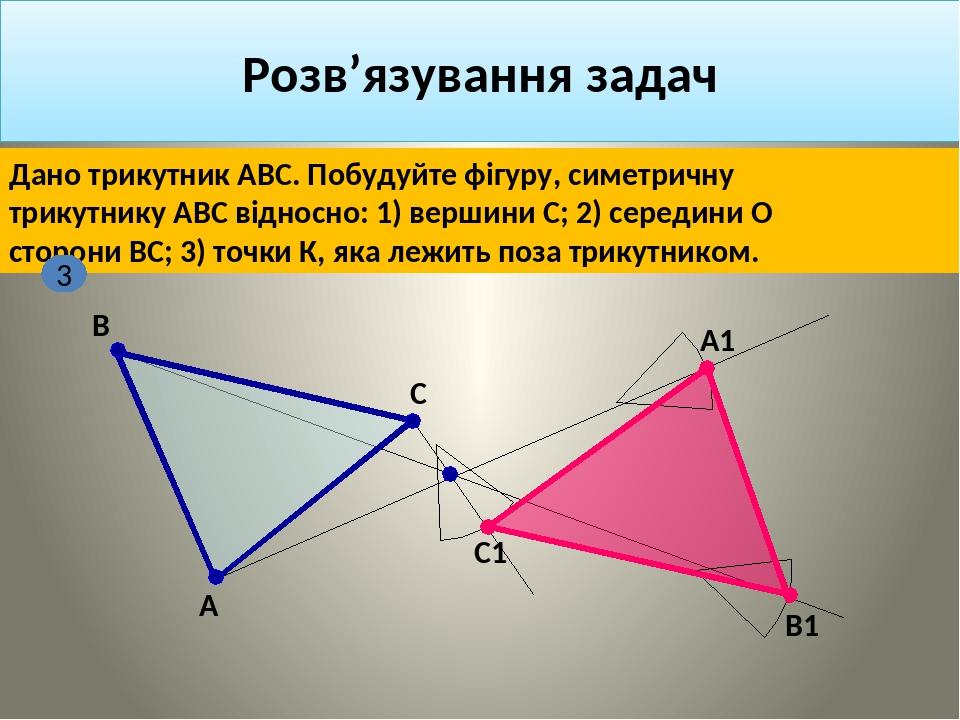
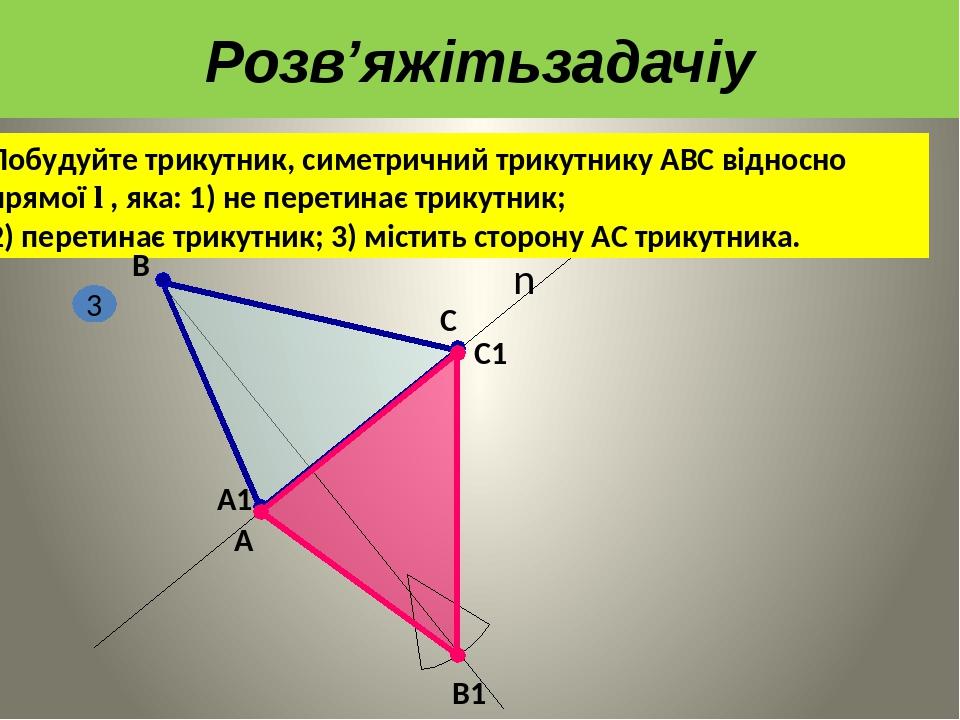
8 геометрія Тема: «Розв”язування задач»

Задача. Ремонтуючи клас влітку, необхідно було розрахувати кількість фарби для підлоги. Скільки потрібно банок по 2,8 кг, якщо на 1 м² приблизно витрачається 120 г фарби.

Що необхідно, щоб розв’язати цю задачу? Правильно, знати площу підлоги. Якщо довжина класу 11 м, а ширина 6 м, то площа 66 м². Отже, потрібно 120 г * 66 м²= 7920 г = 7,92 кг фарби. А банок потрібно 7,92 : 2,8 » 2,82 » 3

1. Сторони квадратів 100 м і 150 м. Знайдіть сторону третього квадрата, площа якого дорівнює сумі площ двох заданих.

Розв’язання

S₁ = 100² = 10000 (м²), S₂ = 150² = 22500 (м²), S₃ = 10000 + 22500 = 32500 (м²).

а₃ = √32500 = 50√13 ≈ 180 (м).

2. Знайти сторони прямокутника, якщо його периметр 74 см, а площа 3 м².

Дано: АВСD - прямокутник;

Р = 74 дм,

S = 3 м².

Знайти: сторони.

Розв’язання.

Позначимо сторони АВ = а, ВС = b, тоді складемо і розв’яжемо систему рівнянь:

2(а + b)2 = 74,

а + b = 37,

аb = 300; аb = 300; b(37 – b) = 300;

Розв’яжемо квадратне рівняння: b² – 37b + 300 = 0, b₁ = 12, або b₂ = 25.

а₁ = 25, або а₂ = 12.

Отже, сторони прямокутника 12 дм і 25 дм.

Відповідь: 12 дм, 25 дм.

3. Україна – одна з найбільших європейських держав, її площа 604 тис. км². На скільки квадратних кілометрів площа України більша за площу Франції (544 тис. км²), Швеції (450 тис. км²)?

Відповідь: на 60 тис. км², на 154 тис. км².

4. Сад має форму прямокутника із сторонами 80 і 25 м. Половину усієї площі засаджено яблунями. Для кожної яблуні відведено 40 м². Скільки яблунь у саду?

Відповідь: 50 яблунь.

5. Щоб посіяти гречку на 1 м² потрібно 15 г гречки. Скільки грамів гречки потрібно, щоб засіяти ділянку 40 м²?

Відповідь: 600 г.

Домашнє завдання: опрацювати п 19-20 № 653, 677 і

Розшифруйте кросворд, дайте відповіді на запитання:

По горизонталі:

Одиниця вимірювання площі
Що знаходиться для прямокутника як добуток його довжини і ширини
Як звали жінку, яка стала причиною Троянської війни?
Чому дорівнює площа прямокутника із сторонами 0,5 дм і 1,6 см.

По вертикалі:

Хто написав Іліаду?

Як називаються фігури, що мають рівні площі?
Чому дорівнює площа прямокутного трикутника із катетами 5 см і 80 мм?
Як називається одиниця вимірювання кількості жіночої краси?

	¹	⁵
²
		⁴	⁶	⁷
³

9 клас геометрія Тема "Центральна і осьова симетрія"

СЛАЙД № 3

КОМПЕТЕНТНІСТЬ ОБДАРОВАНІСТЬ РАДІСТЬ УСПІХ У Р О К

СЛАЙД № 4

Формування вмінь застосовувати вивчені поняття та властивості до розв’язуванні задач Мета уроку: формування поняття симетрії відносно точки та прямої вичення їх властивостей відносно точки та прямої . Розвивати навчальні інтереси, просторову уяву уміння аналізувати,систематизувати,робити висновки. Виховувати культу спілкування формувати навички аналізу,систематизації,узагальнення. Виховувати уміння тактовно висловлювати свою думку

СЛАЙД № 5

Бліц опитування: 1) Яке перетворення називається переміщенням (рухом)? 1) Перетворення називається переміщенням (рухом), якщо воно зберігає відстань між точками. 2) При переміщенні у які точки переходять точки, що лежать на прямій? 2) При переміщенні точки, що лежать на прямій переходять у точки, що лежать на прямій, і зберігається порядок їх взаємного розміщення. 3 ) У які фігури переходять прямі, промені, відрізки під час переміщення? 3 ) Переміщення (рух) прямі переводить у прямі, промені у промені, відрізки у рівні їм відрізки.

СЛАЙД № 6

Симетрія відносно точки Перетворення симетрії відносно точки О називають таке перетворення фігури F у фігуру F’ , унаслідок якого кожна точка Х фігури F переходить у точку Х’ фігури F’ симетричну точці Х відносно точки О. При цьому фігури F i F’називають симетричними відносно точки О. Фігури F і F’ симетричні відносно точки О Якщо перетворення симетрії відносно точки О переводить фігуру F у себе, то така фігура називається центрально-симетричною, а точка О – центром симетрії фігури F.

СЛАЙД № 7

Симетрія відносно точки. Симетрія відносно прямої. Симетрія (від грецького “симетріа”) – узгодженість розмірів, однаковість у розміщенні частин. Точки Х і Х’ називаються симетричними відносно точки О, якщо точка О – середина відрізка ХХ’ Точки Х і Х’симетричні відносно точки О Симетрію відносно точки також називають центральною симетрією.

СЛАЙД № 8

ТЕОРЕМА (основна властивість центральної симетрії) Центральна симетрія є переміщенням. Нехай унаслідок центральної симетрії відносно точки О точки X і Y переходять у точки Х’ і Y’ відповідно. Розглянемо загальний випадок (рис.) коли точки О, Х і Y не лежать на одній прямій. Трикутники ХОY і Х’О’Y’ рівні за першою ознакою, отже, ХY=Х’Y’. Таким чином, центральна симетрія зберігає відстань між точками, отже, є переміщенням. Теорема доведена.

СЛАЙД № 9

Розв’яжітьзадачі: №1 Відрізок АС і його середина В внаслідок переміщення переходить у відоізок А’C’ і точку B’ відповідно. Знайдіть довжину відрізка А’С’, якщо АВ=30см. №2 Під час переміщення чотирикутника АВСД отримали квадрат А’В’С’Д’. Визначте довжину діагоналі ВД, якщо А’С’=4см. Симетрію відносно точки також називають центральною симетрією.

СЛАЙД № 10

А В n Осьова симетрія зберігає відстані між точками. Осьова симетрія – рух (переміщення). Осьова симетрія має всі властивості руху. А1 В1 Осьова симетрія

СЛАЙД № 11

А В n А1 В1 Осьова симетрія має всі властивості руху: Відрізки переходять у рівні їм відрізки. Осьова симетрія

СЛАЙД № 12

А В n А1 В1 Осьова симетрія має всі властивості руху: Відрізки переходять у рівні їм відрізки. Осьова симетрія

СЛАЙД № 13

А В О А1 В1 Центральна симетрія має всі властивості руху: Промені переходять у промені. Центральна симетрія

СЛАЙД № 14

А В О Центральна симетрія зберігає відстані між точками. Центральна симетрія – рух (переміщення). Центральна симетрія має всі властивості руху. А1 В1 Центральна симетрія Відрізки переходять у рівні їм відрізки. Промені переходять у промені.

СЛАЙД № 15

Побудуйте трикутник, симетричний трикутнику АВС відносно прямої l , яка: 1) не перетинає трикутник; 2) перетинає трикутник; 3) містить сторону АС трикутника. А В С В1 А1 С1 1 n Розв’яжітьзадачіу

СЛАЙД № 16

Розв’язування задач Дано трикутник АВС. Побудуйте фігуру, симетричну трикутнику АВС відносно: 1) вершини С; 2) середини О Сторони ВС; 3) точки К, яка лежить поза трикутником. А В С В1 А1 С1 О 2

СЛАЙД № 17

Дано трикутник АВС. Побудуйте фігуру, симетричну трикутнику АВС відносно: 1) вершини С; 2) середини О сторони ВС; 3) точки К, яка лежить поза трикутником. А В С В1 А1 С1 3 Розв’язування задач

СЛАЙД № 18

Побудуйте трикутник, симетричний трикутнику АВС відносно прямої l , яка: 1) не перетинає трикутник; 2) перетинає трикутник; 3) містить сторону АС трикутника. А В С В1 С1 А1 3 n Розв’яжітьзадачіу

СЛАЙД № 19

Доведення Нехай унаслідок осьової симетрії відносно прямої l точки Х і У переходять у точки Х’ і У’ відповідно. Введемо систему координат так, щоб пряма l збіглася з віссю Oy (рис.). Тоді внаслідок симетрії відносно цієї прямої точки Х(х1; у1) і Y(х2; у2) перейдуть у точки Х’(х1; у1) і Y‘(-х2; у2) відповідно. За формулою відстані між точками маємо: , , отже, ХУ=Х’У’ Таким чином, осьова симетрія зберігає відстань між точками, тобто є переміщенням. Теорему доведено. ТЕОРЕМА (основна властивість осьової симетрії) Осьова симетрія є переміщенням.

Домашнє завдання; опрацювати п 18, п 19(ст 175-177) №18.12, 18.20,19.17