9 клас геометрія Тема "Центральна і осьова симетрія"
КОМПЕТЕНТНІСТЬ ОБДАРОВАНІСТЬ РАДІСТЬ УСПІХ У Р О К
Формування вмінь застосовувати вивчені поняття та властивості до розв’язуванні задач Мета уроку: формування поняття симетрії відносно точки та прямої вичення їх властивостей відносно точки та прямої . Розвивати навчальні інтереси, просторову уяву уміння аналізувати,систематизувати,робити висновки. Виховувати культу спілкування формувати навички аналізу,систематизації,узагальнення. Виховувати уміння тактовно висловлювати свою думку

Бліц опитування: 1) Яке перетворення називається переміщенням (рухом)? 1) Перетворення називається переміщенням (рухом), якщо воно зберігає відстань між точками. 2) При переміщенні у які точки переходять точки, що лежать на прямій? 2) При переміщенні точки, що лежать на прямій переходять у точки, що лежать на прямій, і зберігається порядок їх взаємного розміщення. 3 ) У які фігури переходять прямі, промені, відрізки під час переміщення? 3 ) Переміщення (рух) прямі переводить у прямі, промені у промені, відрізки у рівні їм відрізки.
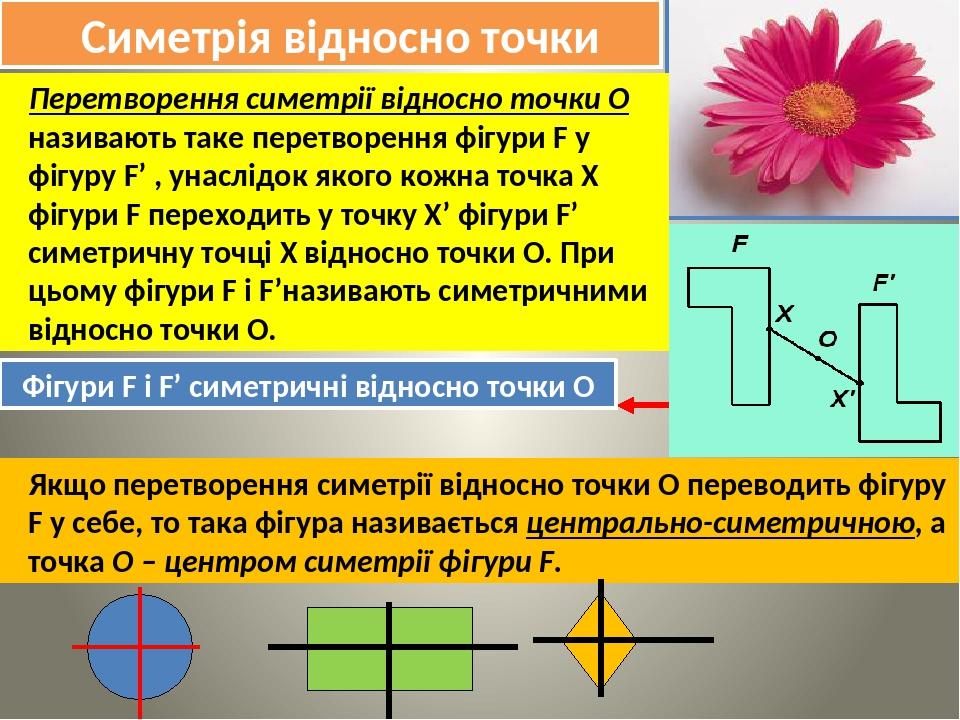
Симетрія відносно точки Перетворення симетрії відносно точки О називають таке перетворення фігури F у фігуру F’ , унаслідок якого кожна точка Х фігури F переходить у точку Х’ фігури F’ симетричну точці Х відносно точки О. При цьому фігури F i F’називають симетричними відносно точки О. Фігури F і F’ симетричні відносно точки О Якщо перетворення симетрії відносно точки О переводить фігуру F у себе, то така фігура називається центрально-симетричною, а точка О – центром симетрії фігури F.
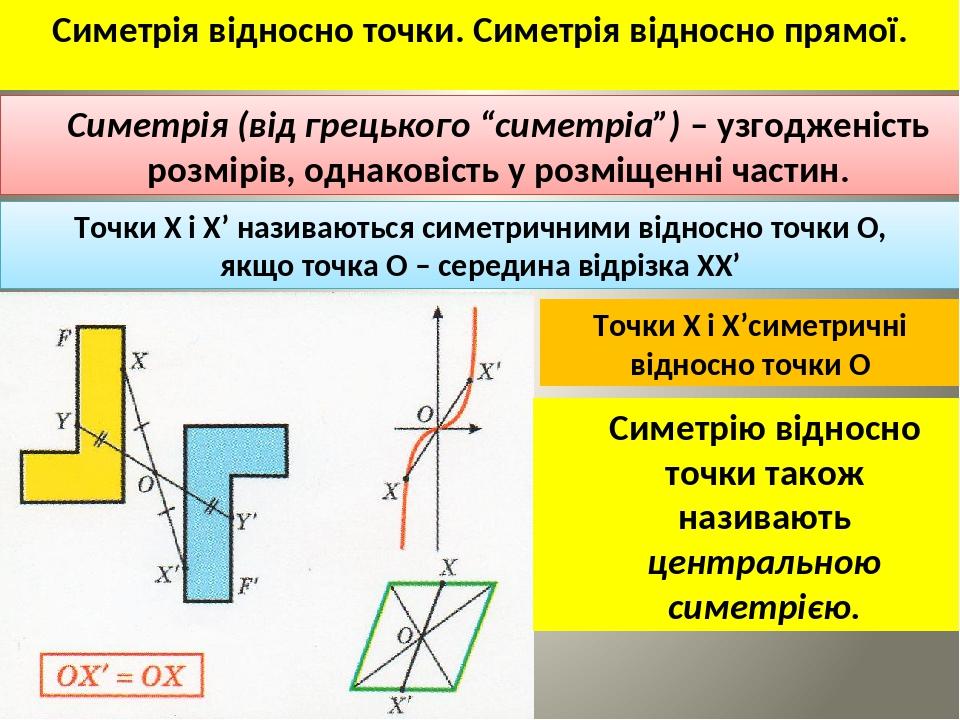
Симетрія відносно точки. Симетрія відносно прямої. Симетрія (від грецького “симетріа”) – узгодженість розмірів, однаковість у розміщенні частин. Точки Х і Х’ називаються симетричними відносно точки О, якщо точка О – середина відрізка ХХ’ Точки Х і Х’симетричні відносно точки О Симетрію відносно точки також називають центральною симетрією.
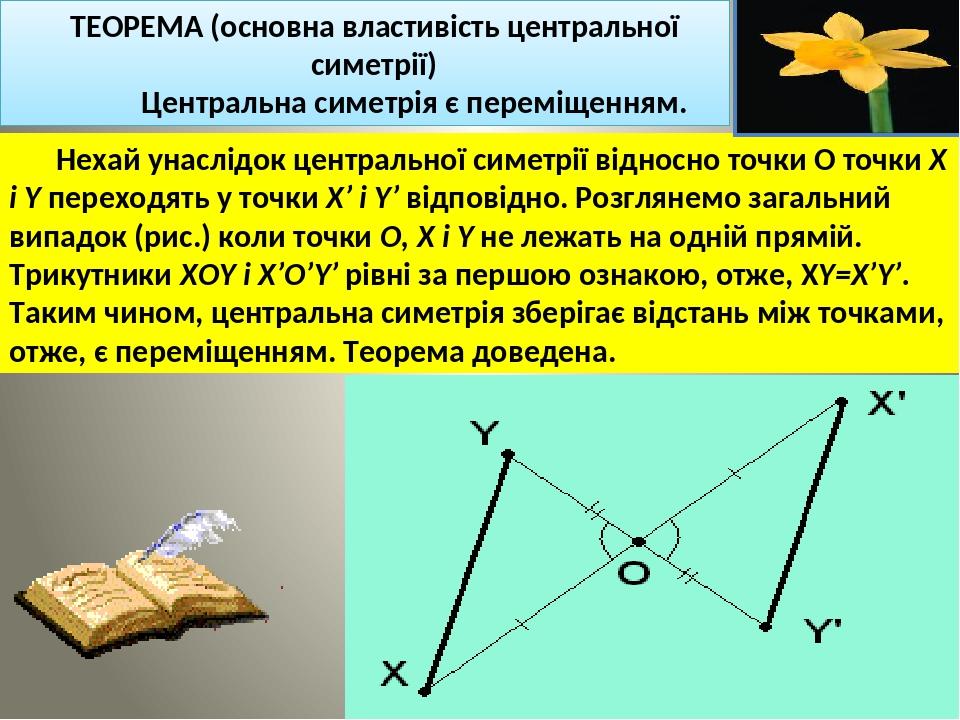
ТЕОРЕМА (основна властивість центральної симетрії) Центральна симетрія є переміщенням. Нехай унаслідок центральної симетрії відносно точки О точки X і Y переходять у точки Х’ і Y’ відповідно. Розглянемо загальний випадок (рис.) коли точки О, Х і Y не лежать на одній прямій. Трикутники ХОY і Х’О’Y’ рівні за першою ознакою, отже, ХY=Х’Y’. Таким чином, центральна симетрія зберігає відстань між точками, отже, є переміщенням. Теорема доведена.

Розв’яжітьзадачі: №1 Відрізок АС і його середина В внаслідок переміщення переходить у відоізок А’C’ і точку B’ відповідно. Знайдіть довжину відрізка А’С’, якщо АВ=30см. №2 Під час переміщення чотирикутника АВСД отримали квадрат А’В’С’Д’. Визначте довжину діагоналі ВД, якщо А’С’=4см. Симетрію відносно точки також називають центральною симетрією.
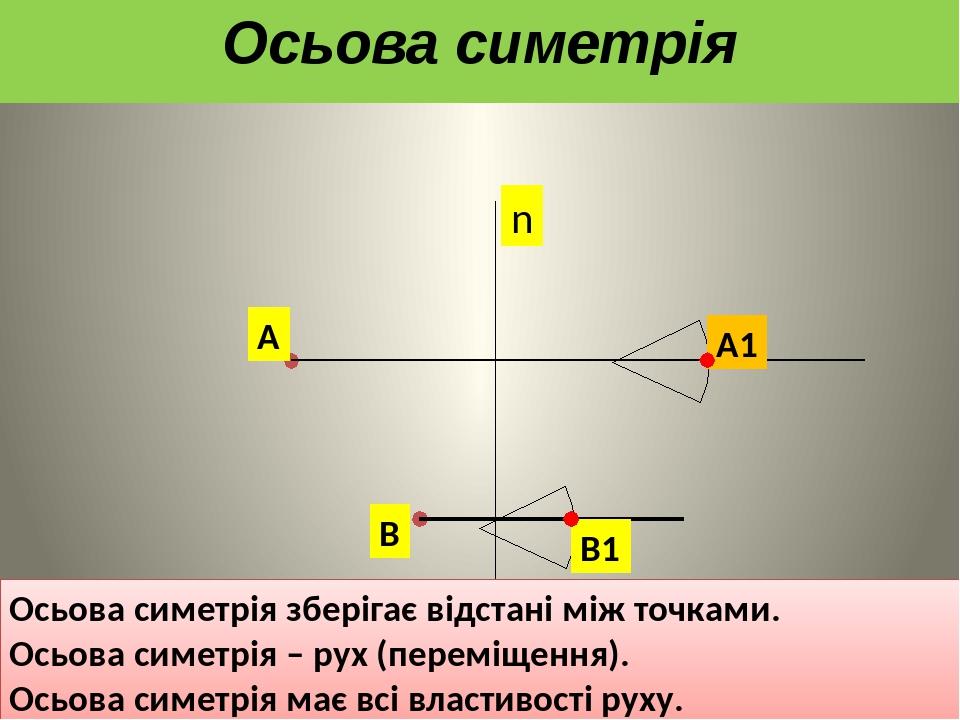
А В n Осьова симетрія зберігає відстані між точками. Осьова симетрія – рух (переміщення). Осьова симетрія має всі властивості руху. А1 В1 Осьова симетрія
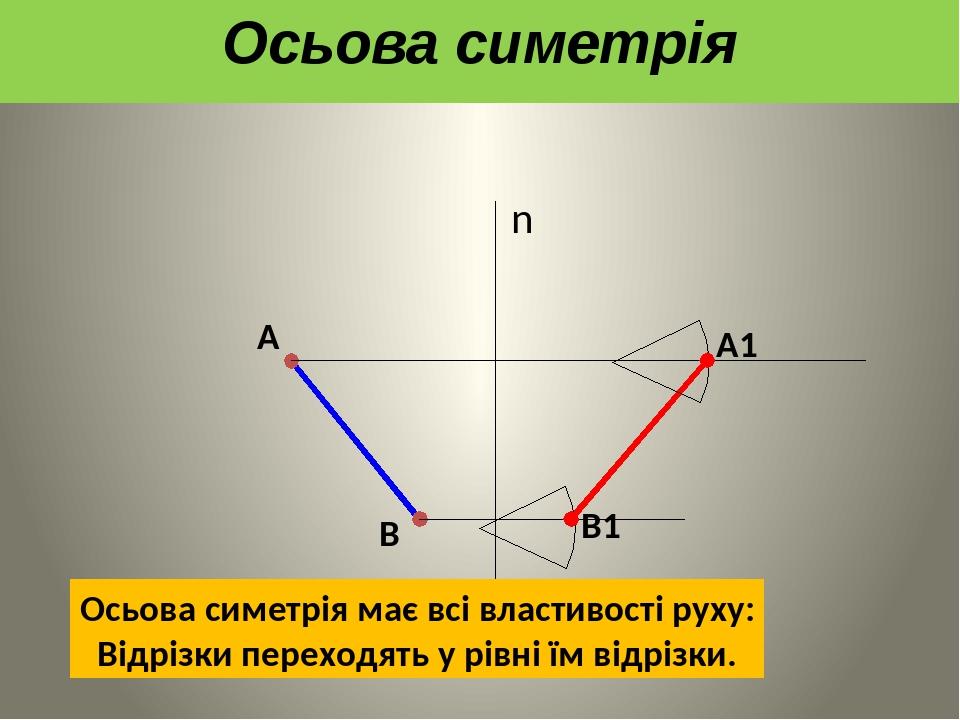
А В n А1 В1 Осьова симетрія має всі властивості руху: Відрізки переходять у рівні їм відрізки. Осьова симетрія
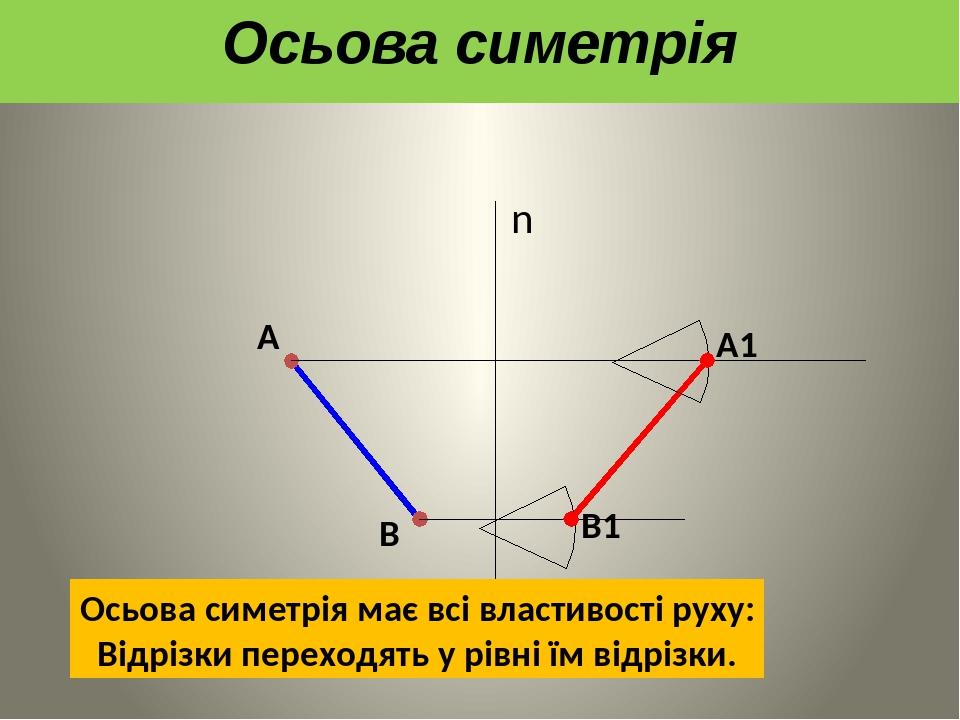
А В n А1 В1 Осьова симетрія має всі властивості руху: Відрізки переходять у рівні їм відрізки. Осьова симетрія
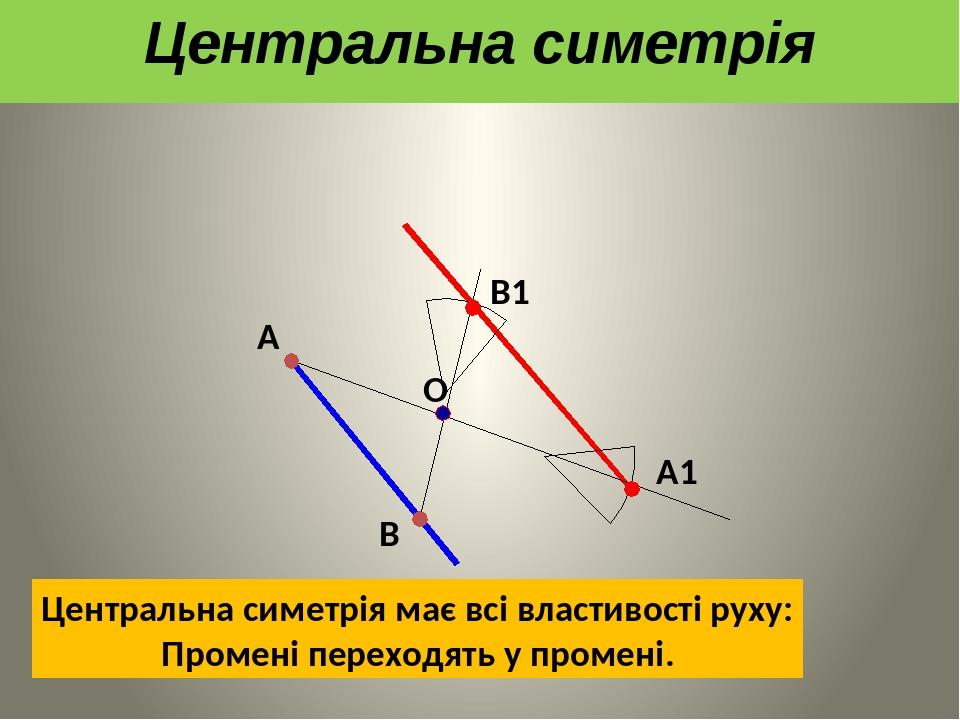
А В О А1 В1 Центральна симетрія має всі властивості руху: Промені переходять у промені. Центральна симетрія
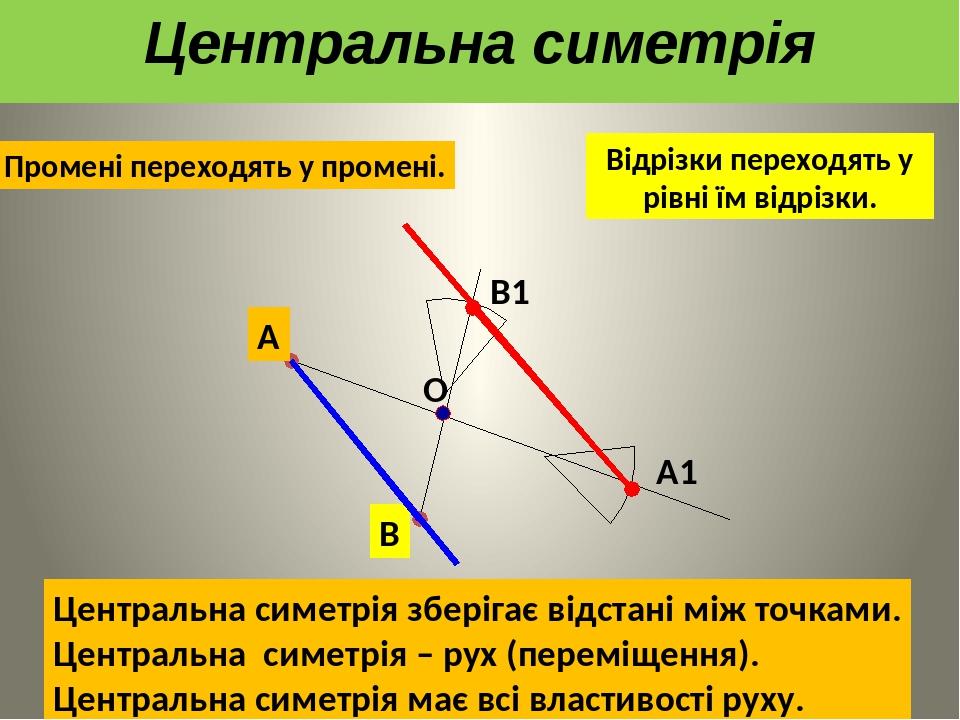
А В О Центральна симетрія зберігає відстані між точками. Центральна симетрія – рух (переміщення). Центральна симетрія має всі властивості руху. А1 В1 Центральна симетрія Відрізки переходять у рівні їм відрізки. Промені переходять у промені.
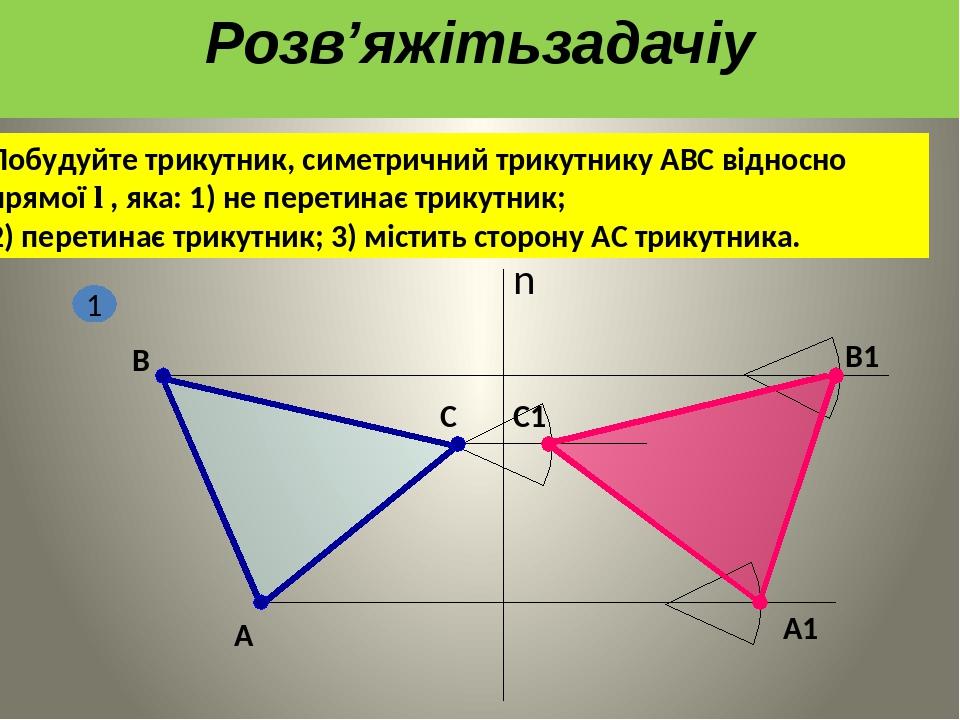
Побудуйте трикутник, симетричний трикутнику АВС відносно прямої l , яка: 1) не перетинає трикутник; 2) перетинає трикутник; 3) містить сторону АС трикутника. А В С В1 А1 С1 1 n Розв’яжітьзадачіу
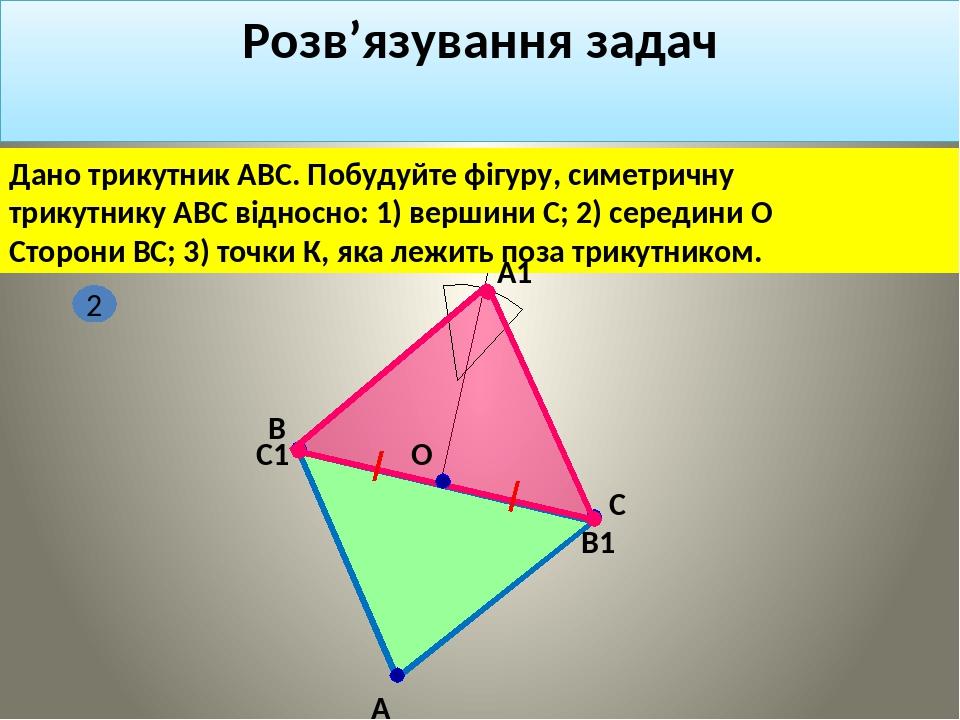
Розв’язування задач Дано трикутник АВС. Побудуйте фігуру, симетричну трикутнику АВС відносно: 1) вершини С; 2) середини О Сторони ВС; 3) точки К, яка лежить поза трикутником. А В С В1 А1 С1 О 2
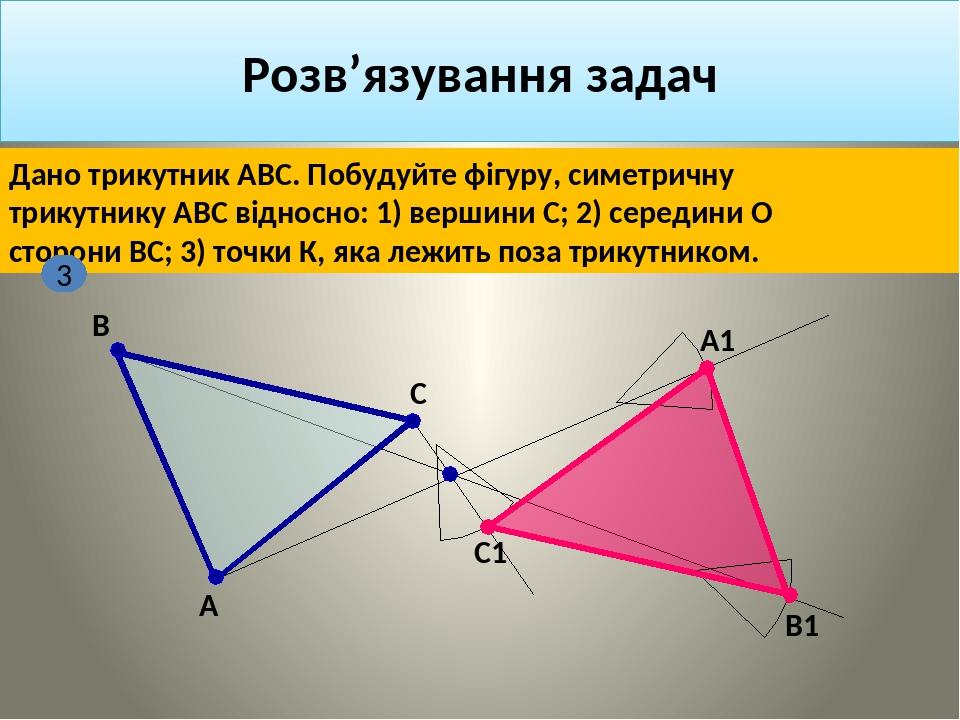
Дано трикутник АВС. Побудуйте фігуру, симетричну трикутнику АВС відносно: 1) вершини С; 2) середини О сторони ВС; 3) точки К, яка лежить поза трикутником. А В С В1 А1 С1 3 Розв’язування задач
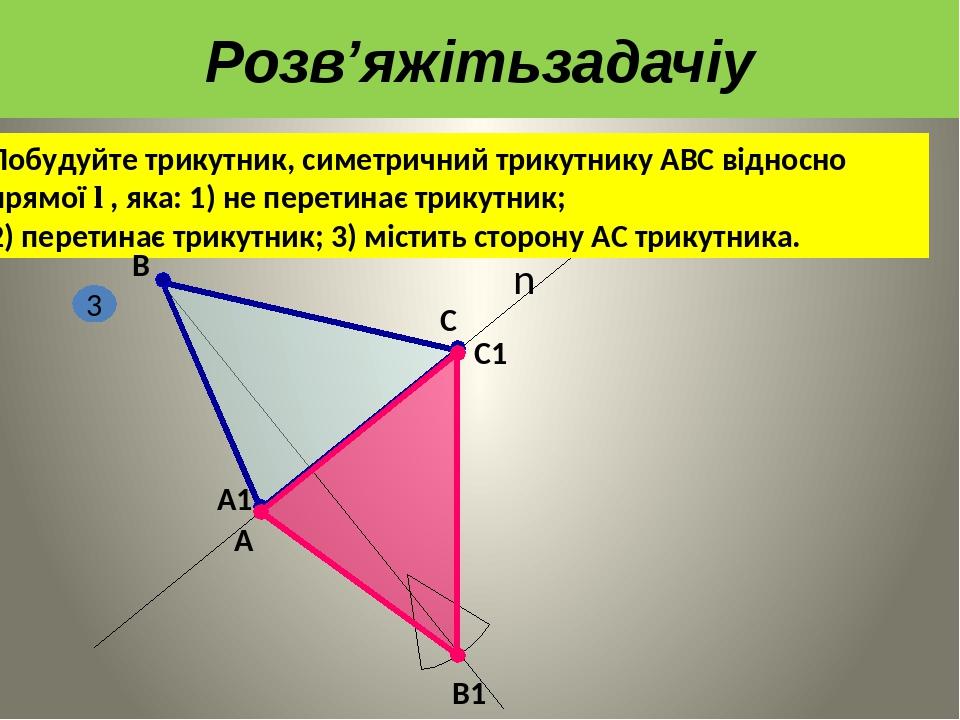
Побудуйте трикутник, симетричний трикутнику АВС відносно прямої l , яка: 1) не перетинає трикутник; 2) перетинає трикутник; 3) містить сторону АС трикутника. А В С В1 С1 А1 3 n Розв’яжітьзадачіу

Доведення Нехай унаслідок осьової симетрії відносно прямої l точки Х і У переходять у точки Х’ і У’ відповідно. Введемо систему координат так, щоб пряма l збіглася з віссю Oy (рис.). Тоді внаслідок симетрії відносно цієї прямої точки Х(х1; у1) і Y(х2; у2) перейдуть у точки Х’(х1; у1) і Y‘(-х2; у2) відповідно. За формулою відстані між точками маємо: , , отже, ХУ=Х’У’ Таким чином, осьова симетрія зберігає відстань між точками, тобто є переміщенням. Теорему доведено. ТЕОРЕМА (основна властивість осьової симетрії) Осьова симетрія є переміщенням.
Домашнє завдання; опрацювати п 18, п 19(ст 175-177) №18.12, 18.20,19.17
Комментариев нет:
Отправить комментарий